Formula For Force

The concept of force is fundamental in physics, serving as the cornerstone for understanding motion, interactions, and the very fabric of the universe. From the gravitational pull that keeps us grounded to the electromagnetic forces governing chemical bonds, forces are omnipresent and multifaceted. This article delves into the formula for force, exploring its historical evolution, theoretical underpinnings, and practical applications across various domains.
Historical Evolution of Force Concepts

The understanding of force has evolved significantly over centuries. Aristotle’s initial theories, which linked force to the natural place of objects, were revolutionized by Galileo Galilei and Isaac Newton. Newton’s seminal work, Philosophiæ Naturalis Principia Mathematica (1687), introduced the three laws of motion, laying the groundwork for classical mechanics.
Key Milestones in Force Understanding
- Aristotle (384–322 BCE): Proposed that objects tend toward their natural place, with force required to maintain motion.
- Galileo Galilei (1564–1642): Challenged Aristotelian views, demonstrating that objects maintain motion without continuous force.
- Isaac Newton (1642–1727): Formulated the laws of motion and universal gravitation, quantifying force as a product of mass and acceleration.
- 20th Century: Einstein's relativity and quantum mechanics expanded force concepts, incorporating fields and particle interactions.
The Fundamental Formula: Newton’s Second Law

At the heart of classical mechanics lies Newton’s second law of motion, which defines force as:
F = m * a
Where:
- F is the force applied (in Newtons, N)
- m is the mass of the object (in kilograms, kg)
- a is the acceleration produced (in meters per second squared, m/s²)
This equation encapsulates the relationship between force, mass, and acceleration, providing a quantitative framework for analyzing motion. For instance, applying a force of 10 N to a 2 kg object results in an acceleration of 5 m/s².
Beyond Newton: Forces in Modern Physics
While Newton’s laws remain highly accurate for everyday phenomena, modern physics has expanded the concept of force to include:
Electromagnetic Forces
Governed by Coulomb’s law, electromagnetic forces arise from the interaction of charged particles. The formula is:
[ F = k \cdot \frac{|q_1 \cdot q_2|}{r^2} ]
Where: - ( F ) is the force (in Newtons) - ( k ) is Coulomb’s constant (( 8.99 \times 10^9 \, \text{N·m²/C²} )) - ( q_1 ) and ( q_2 ) are the charges (in Coulombs) - ( r ) is the distance between charges (in meters)
Pros:
Explains atomic bonding, electrical circuits, and light-matter interactions.
Cons:
Does not account for relativistic effects or quantum phenomena.
Gravitational Forces
Newton’s law of universal gravitation describes the force between two masses:
[ F = G \cdot \frac{m_1 \cdot m_2}{r^2} ]
Where: - ( F ) is the force (in Newtons) - ( G ) is the gravitational constant (( 6.674 \times 10^{-11} \, \text{N·m²/kg²} )) - ( m_1 ) and ( m_2 ) are the masses (in kilograms) - ( r ) is the distance between centers (in meters)
Strong and Weak Nuclear Forces
These forces operate at atomic scales, governing particle interactions within nuclei. While not described by simple formulas, they are critical for nuclear stability and radioactive decay.
Practical Applications of Force Formulas
Understanding force formulas is essential across disciplines:
Engineering and Technology
- Structural Design: Calculating forces ensures buildings and bridges withstand loads.
- Automotive Industry: Force analysis optimizes vehicle performance and safety.
- Aerospace: Thrust and drag forces determine aircraft and spacecraft trajectories.
In engineering, precise force calculations prevent failures and enhance efficiency.
Forces in Everyday Life
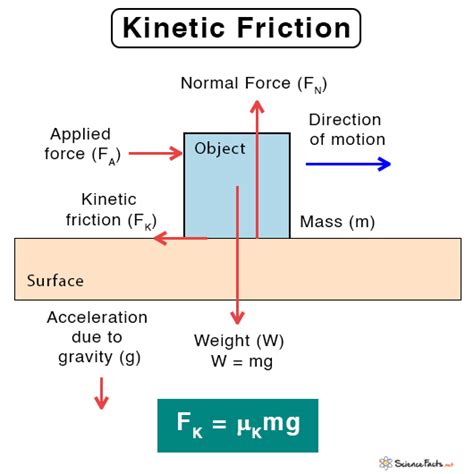
Forces are integral to daily experiences:
- Friction: Opposes motion, governed by ( F = μ \cdot N ), where ( μ ) is the coefficient of friction and ( N ) is the normal force.
- Tension: Acts along ropes or cables, balancing forces in systems like pulleys.
- Air Resistance: Depends on velocity and object shape, affecting falling objects and vehicles.
Comparative Analysis: Classical vs. Modern Force Concepts
| Aspect | Classical Mechanics | Modern Physics |
|---|---|---|
| Framework | Newton's laws, deterministic | Relativity, quantum mechanics, probabilistic |
| Force Nature | Direct interaction | Field-mediated (e.g., electromagnetic, gravitational) |
| Applicability | Macroscopic, low speeds | All scales, high speeds/energies |

Future Trends: Forces in Emerging Technologies
Advancements in nanotechnology, quantum computing, and space exploration demand deeper force understanding. For instance, manipulating Casimir forces could enable micro-scale devices, while harnessing gravitational waves may revolutionize astronomy.
As technology advances, force formulas will continue to evolve, bridging theoretical physics and practical applications.
FAQ Section
What is the unit of force?
+The SI unit of force is the Newton (N), equivalent to kg·m/s².
How does force differ from energy?
+Force is a push or pull causing acceleration, while energy is the capacity to do work, measured in Joules (J).
Can force exist without motion?
+Yes, balanced forces (e.g., static objects) result in no net motion despite force presence.
What is the strongest fundamental force?
+The strong nuclear force is the strongest, binding quarks into protons and neutrons.
How does relativity affect force?
+Relativity modifies force calculations at high speeds, incorporating mass-energy equivalence and time dilation.
Conclusion: The Universal Language of Force
From Newton’s elegant equation to the complexities of modern physics, the formula for force remains a cornerstone of scientific inquiry. Whether designing bridges or exploring the cosmos, understanding forces empowers us to decipher the universe’s mechanics. As we continue to unravel nature’s secrets, the concept of force will undoubtedly remain a guiding principle, bridging theory and practice in the pursuit of knowledge.



